
SALA 11 – MOMENTO ANGULAR V4.3

“Tengo una vara uniforme que gira en un plano horizontal alrededor de un eje vertical que pasa por su centro. Como la fuerza vertical que ejerce el eje pasa por el eje, no produce torque, pero la gravedad sí produce torques externos. Por ejemplo, un trozo de un extremo siente un peso y tiene un brazo. Entonces no hay conservación del momento angular”. Si el eje pasa por el centro de masa de la vara, la gravedad NO produce un torque neto. El torque que siente un trozo en un extremo es igual pero de signo opuesto al que siente un trozo en el extremo opuesto. La fuerza neta que produce la gravedad sobre un cuerpo siempre actúa sobre su centro de masa de tal forma que si este centro de masa está sobre el eje, el torque es cero. El momento angular SI se conserva.
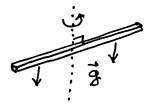
“Tengo dos discos idénticos uniformes. El inferior está en reposo y el superior gira con wi alrededor de un eje común. Entonces el superior toca y queda instantáneamente pegado al inferior, de tal manera que ahora el par gira con wf. Hay conservación del momento angular. Puesto que cuando se tocan no resbalan, no hay fricción cinética, y entonces hay conservación de la energía mecánica.” Aunque hay conservación de momento angular, la energía mecánica disminuye. La situación es equivalente a una colisión perfectamente inelástica.
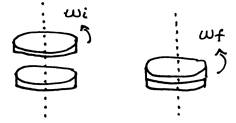
“Cuando un gimnasta gira y luego acerca sus brazos a su cuerpo hay conservación del momento angular y hay conservación de la energía mecánica”. Aunque hay conservación del momento angular, la energía mecánica aumenta, y el aumento proviene de energía química producida por los músculos de sus brazos.
"Si un cuerpo tiene momento angular es porque está rotando alrededor de un eje". Tiene momento angular si el producto vectorial de su vector posición por su momento lineal (Là = rà × pà) respecto al origen de un marco inercial es diferente de cero. Por ejemplo, un cuerpo moviéndose en línea RECTA puede tener un momento angular.
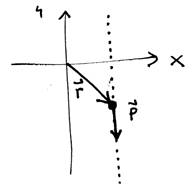
“Puesto que la magnitud del momento angular es igual a r p senq , entonces rà × pà = pà × rà “. No, a diferencia del producto escalar de vectores, en el producto vectorial de vectores el orden es importante. Al invertir el orden se invierte el sentido del vector resultante: rà × pà = - pà × rà .
“Cuando rà y pà yacen en el plano XY puedo usar un determinante de dimensión 2 × 2 para calcular el producto vectorial”. No, siempre tienes que usar el determinante completo, de dimensión 3 × 3.
"El momento angular de un cuerpo siempre es igual a la inercia rotacional multiplicada por la velocidad angular (L® = I wà )". Correcto para cuerpos rígidos que giran alrededor de uno de sus “ejes principales” (tales como los ejes de simetría de un disco), pero no es correcto en general. Los casos más generales requieren tratamientos más sofisticados y los vectores momento angular y velocidad angular no tienen que ser paralelos. Por ejemplo, considera el momento angular de una masa puntual respecto del extremo fijo de la cuerda del péndulo cónico. Tampoco es general la definición de energía cinética rotacional como un medio del producto de la inercia rotacional y el cuadrado de la velocidad angular (K = ½ I ω2 ).
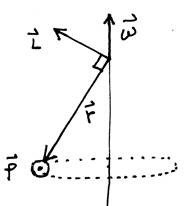
"El torque y el momento angular se calculan respecto al eje de rotación que pasa por el centro de masa". Los calculas respecto a un mismo PUNTO cualquiera en un marco inercial, usualmente su origen. En general, NO tiene que existir un eje de rotación. El cuerpo NO tiene que estar rotando alrededor de un eje. Si hay un eje de rotación, este NO tiene que pasar por el centro de masa. Si el punto es un punto fijo al centro de masa del cuerpo, es un caso especial en donde el marco no tiene que ser inercial, o sea, el centro de masa puede acelerar.
“Si es conveniente, puedo calcular el torque respecto a un punto diferente al del momento angular”. La ecuación de movimiento iguala el vector torque neto a la derivada respecto al tiempo del vector momento angular (τ→ neto = dL→ /dt) , ambos calculados respecto al MISMO punto en un mismo marco de referencia.
“Si se calcula un torque neto igual a cero es porque hay conservación de momento angular respecto a cualquier punto”. Hay conservación de momento angular respecto al mismo punto que se usó para calcular el torque, pero no necesariamente respecto a otros puntos, pues tanto el torque como el momento angular cambian cuando se cambia el punto respecto al cual se calculan. Nota que esto no es así para el cálculo de fuerzas.
“La ecuación de movimiento para rotaciones es una ley física nueva”. No, se deduce a partir de la segunda ley de Newton.
“La fuerza normal sobre un cuerpo siempre actúa a lo largo de una línea que pasa por su centro”. Para situaciones en donde tomamos los cuerpos como masas puntuales, no importa el punto donde actúa una fuerza. Si se considera la extensión real de los cuerpos (por ejemplo, para calcular torques) es importante determinar este punto, y en general, una fuerza normal sobre un cuerpo NO actúa sobre su centro geométrico o su centro de masa.
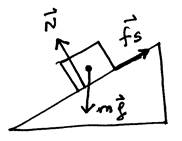
“Para que un cuerpo esté en equilibrio estático, la fuerza normal tiene que pasar por el centro de masa del cuerpo”. No necesariamente. Por ejemplo, un bloque en reposo sobre un plano inclinado tiene una fuerza normal que NO pasa por el centro de masa.
“La fuerza que ejerce una bisagra sobre una puerta siempre está en el plano de la puerta”. No es obvia la dirección de esta fuerza, pues depende de la situación particular. En el caso más general debes suponer que la fuerza tiene dos componentes perpendiculares al eje de la bisagra y una componente en el eje. La solución correcta del problema dará los valores correctos de las componentes.
"La conservación del momento lineal se deriva de las leyes de Newton, y también lo es la conservación del momento angular". Para la conservación del momento angular también se necesita el hecho que las fuerzas fundamentales son centrales. Hoy sabemos que los principios de conservación de energía, momento lineal y momento angular tienen validez universal, más allá del reino de Newton, y por esto son más fundamentales que las leyes de Newton. Hoy también sabemos que los campos (como el gravitacional y el electromagnético) también poseen momento lineal y angular.