SALA 4 - APLICACIONES DE LAS LEYES DE NEWTON                     v4.3

"Para resolver un problema en mecánica, lo único que necesito es aplicar las tres leyes de Newton". También necesitas una o más relaciones dadas por las condiciones de confinamiento o ligadura de los cuerpos, que no las puedes derivar de las leyes de Newton. Por ejemplo, si tienes un libro en reposo sobre una mesa, su aceleración es cero. Esta es una relación de confinamiento que no sale de las leyes de Newton, sino que es una información adicional.

“No sé cómo identificar mi sistema de partículas”. Escoge el mínimo número de partículas relevantes, pero no menos. El ambiente será representado por las fuerzas que ejerce sobre las partículas relevantes. Hay libertad de escoger el sistema, aunque el problema se simplifica si solamente se incluyen las partículas relevantes.

“Un libro en reposo sobre una mesa constituye un sistema compuesto de varios cuerpos”. Un sistema físico en general consiste de una o más partículas y su ambiente. Aquí no estas tomando en cuenta que el libro está compuesto de muchas partículas unidas como un cuerpo rígido a través de fuerzas internas y tomas el libro como una masa puntual. El ambiente lo constituye la mesa y el campo gravitacional producido por la tierra. No te interesan la mesa ni la tierra y te concentras en un diagrama de fuerzas sobre el libro. Si para analizar una situación necesitas hacer varios diagramas de fuerzas es porque el sistema que tomas está compuesto por varios cuerpos, y en esos casos es necesario usar la tercera ley de Newton y relaciones de ligadura entre los cuerpos.

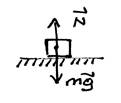
 “Para un libro en reposo sobre una mesa, escribo N^à – mg^à = 0 (con flechas sobre los vectores N^à y  g^à)”. Debes escribir N^à + m g^à = 0 (con flechas sobre los vectores N^à  y  g^à). La segunda ley estipula la SUMA de los vectores fuerza. No te confundas con la ecuación para las componentes (escalares) de las fuerzas que aquí se escribe N – mg = 0.

"Cuando dibujo los ejes de mi marco de referencia centrados sobre el cuerpo es porque estos ejes están siempre amarrados al cuerpo". No necesariamente. Si el cuerpo acelera, los ejes no pueden estar amarrados al cuerpo, porque entonces no sería un marco de referencia inercial. En este caso imagina que los ejes están en reposo y que en ese instante el centro del cuerpo coincide con el origen.

"En un diagrama de fuerzas para  un cuerpo tengo que poner todas las fuerzas que existan". En este diagrama de fuerzas, también llamado diagrama de “cuerpo libre”, se simboliza el cuerpo como un punto y solamente dibujas los vectores para todas las fuerzas que actúan SOBRE el cuerpo. No pones las fuerzas que el cuerpo hace sobre otros cuerpos.

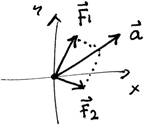
"Hay dos fuerzas F^à₁ y F^à₂ actuando sobre un cuerpo. Entonces F^à₁ = m a^à₁ y F^à₂ = m a^à₂". Aunque existan varias fuerzas sobre un cuerpo, éste solamente puede tener una sola aceleración. La segunda ley se refiere a la fuerza NETA sobre el cuerpo. Debes escribir: F^à neta = F^à₁ + F^à₂ = m a^à, donde las fuerzas y la aceleración son vectores.

"Como la aceleración de un cuerpo debe apuntar en la dirección de la fuerza, un bloque que se desliza y acelera en un plano inclinado sin fricción debe tener tres fuerzas: el peso, la normal y una fuerza en la dirección en que se desliza". La aceleración apunta en la dirección de la fuerza NETA, que es la componente del peso paralela al plano inclinado. Al estudiar mecánica, con excepción de la gravedad, toda fuerza sobre un cuerpo aparece por CONTACTO directo con otro cuerpo que es el responsable de la fuerza. Aquí no hay nada en contacto con el bloque en la dirección que se desliza. Sobre el bloque solamente actúan dos fuerzas: el peso y la normal.

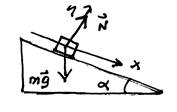
"En casos en dos dimensiones siempre coloco el eje X positivo hacia la derecha y el eje Y positivo hacia arriba". En dos dimensiones las orientaciones de los ejes X y Y son arbitrarias. A veces es conveniente que el eje X no sea horizontal. A menudo es conveniente que la dirección positiva de un eje (por ejemplo, el eje X) apunte en la dirección de la aceleración del cuerpo. Por ejemplo, para un bloque que se desliza por un plano inclinado es conveniente que el eje X apunte en la dirección que se desliza, paralelo al plano, pero inclinado respecto a la horizontal.

“Si al dibujar el vector de una fuerza lo hago en dirección opuesta a la correcta, las respuestas que halle serán incorrectas y tengo que comenzar todo de nuevo”. Luego de dibujar como mejor estimes las direcciones de todas las fuerzas actuando sobre el cuerpo, lo más importante es trabajar algebraicamente, no equivocarte en los signos de las componentes de los vectores de las fuerzas y aplicar correctamente las leyes de Newton. Al final, si una respuesta contiene un signo inesperado, la solución puede ser simplemente cambiar uno o más signos de componentes de fuerzas y corregir la respuesta sin tener que comenzar todo de nuevo. Si has seguido correctamente el procedimiento, el álgebra te ayuda a corregir las direcciones para las fuerzas.

"Si un cuerpo rígido está en contacto con otro cuerpo rígido siempre tiene que existir una fuerza normal entre ellos". No necesariamente. Por ejemplo, imagina dos bloques que reposan colgados de dos cuerdas. Si los dos bloques se tocan pero las cuerdas permanecen verticales, no existe una fuerza normal entre ellos, o sea vale cero. En caso de duda, es mejor suponer que existe la normal y dejar que la solución al problema decida su valor.

“Nunca sé sobre qué punto en el cuerpo debo dibujar cada uno de los vectores fuerza”. Representa el cuerpo como un punto. Las leyes de Newton se refieren a partículas y por ahora suponemos que todos los cuerpos son masas puntuales. El punto de acción de una fuerza solamente será importante cuando estudies torques y equilibrio de cuerpos extensos.

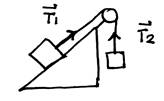
"La tensión en una cuerda tiene la misma magnitud en todo punto de la cuerda". No necesariamente. Solamente se aplica a cuerdas ideales (sin masa) que no sienten fricción en ausencia de poleas o que incluyen poleas ideales (sin masa ni fricción en sus ejes). En la realidad las cuerdas y las poleas tienen masa y existen fricciones, así que la tensión varía entre punto y punto. 

“La magnitud de una tensión en una cuerda nunca cambia con el tiempo”. No siempre. Por ejemplo, la tensión en una cuerda en un péndulo, que cambia con el tiempo y es máxima en el punto más bajo de la trayectoria.

“Para una cuerda ideal tensionada entre dos cuerpos, la fuerza que hace la cuerda sobre cada cuerpo es T ^àvector”. La magnitud de ambas vale T, pero la dirección es diferente para cada fuerza, a veces 180 grados de diferencia, a veces otros ángulos. Para evitar confusiones,  es preferible que definas cada fuerza como un vector con un nombre diferente, aunque sus magnitudes sean iguales, por ejemplo, |T^à₁| = |T^à₂| = T.