
SALA 7 - TRABAJO Y ENERGIA CINETICA v4.3

“Trabajo es fuerza por distancia. Una persona que lleva cargado un bulto entre dos mesas hace un trabajo”. “Fuerza por distancia”es una frase vaga e imprecisa. Para una fuerza constante debes usar la definición que usa el producto escalar del vector fuerza y el vector desplazamiento: WF = Fà·Δ rà. La persona hace una fuerza vertical en un desplazamiento horizontal, así que no hace trabajo.
“La dirección de un trabajo está en la dirección del desplazamiento”. No, el trabajo es un escalar que no tiene dirección, aunque si tiene signo.
“El trabajo hecho por la gravedad sobre una mosca es igual al producto escalar de la fuerza por el desplazamiento causado por la gravedad”. El desplazamiento puede ser cualquiera, debido a varias fuerzas combinadas, aunque el trabajo se calcula para una sola fuerza. Por ejemplo, la mosca puede estar volando desde el piso hasta el techo. El trabajo es igual al producto escalar de la fuerza por el desplazamiento en el caso de fuerzas CONSTANTES durante todo el proceso, pero no para fuerzas variables, tales como las de resortes o de viscosidad o de gravitación en su forma general, en donde la definición de trabajo involucra una integral.
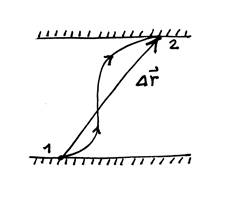
“El trabajo total hecho por la gravedad sobre un proyectil que alcanza una altura h es igual a 2mgh”. El trabajo es cero: -mgh cuando sube, más +mgh cuando baja.
"Si existe una fuerza y un desplazamiento, siempre existe un trabajo". No necesariamente. El trabajo es cero si la fuerza es perpendicular al desplazamiento o si la trayectoria es cerrada y la fuerza es conservativa. Incluso puede llegar a ser cero en una trayectoria no cerrada si la fuerza no es constante, por ejemplo, el trabajo que hace un resorte sobre un bloque entre x = -A y x = A.
"El trabajo hecho por una fuerza sobre un cuerpo es igual al cambio en energía cinética del cuerpo". Solamente es cierto si la fuerza es la UNICA fuerza que hace el trabajo.
“Si solamente una fuerza hace trabajo, ese trabajo siempre aumenta la rapidez del cuerpo”. Solamente si ese trabajo es positivo. Si el trabajo es negativo, la rapidez disminuye.
"El teorema trabajo-energía (W neto = Δ K) solamente se puede aplicar con fuerzas de tipo conservativo". Se aplica con todo tipo de fuerzas, conservativas o disipativas, constantes o variables.
“Si un cuerpo está en equilibrio, entonces no se están realizando trabajos ni potencias”. Puede ser que el cuerpo se mueva con velocidad constante y que existan varias fuerzas que suman cero. En este caso hay desplazamientos, cada fuerza sí hace un trabajo diferente de cero, y sí hay potencias asociadas con cada fuerza. La suma de los trabajos da cero.
“Si el cuerpo permanece en reposo, no existe un trabajo neto en ese marco inercial, pero al verlo desde otro marco inercial en movimiento sí hay desplazamiento y por lo tanto allí si hay un trabajo neto”. No, porque en ninguno de los dos marcos inerciales existe una fuerza neta.
“Una fuerza normal es una fuerza de ligadura y por lo tanto nunca puede realizar un trabajo”. Si el cuerpo se desliza por una superficie fija, y si usas un marco de referencia fijo con la superficie, la fuerza normal siempre es perpendicular al desplazamiento y nunca hace trabajo. La situación es análoga a la de la tensión de una cuerda en un péndulo, y en general para fuerzas de ligadura. Pero si el cuerpo no se desliza, la fuerza normal sí puede hacer un trabajo. Por ejemplo, considera el caso de un bloque fijo respecto a una cuña gracias a la fricción estática, en donde la cuña no está fija y se desliza sobre el piso. Además, en general, si no usas un marco de referencia fijo con la superficie, la normal si puede resultar con un trabajo diferente de cero.
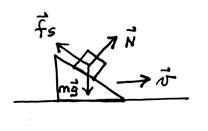
“P =
F®·
v®
da la potencia para una fuerza sobre un cuerpo con cierta velocidad, siempre y
cuando la fuerza sea constante”.
Esta expresión es válida para la potencia instantánea asociada con cualquier
tipo de fuerza, constante o variable, en el instante en que la velocidad del
cuerpo tiene el valor v®
, sin
importar si hay otras fuerzas presentes.